斯坦福NLP教材第5章

洛杉矶的Smilodon和阿根廷的Thylacosmilus两种不同的物种在特定的环境下演化出相似的结构.

出现在相似上下文中的词往往具有相似的意义。这种词语分布方式与它们意义之间的相似性的联系被称为分布假设

嵌入，即直接从文本中的词分布学习到的词的意义的向量表示，研究嵌入及其意义的语言学领域被称为向量语义学。

5.1 Lexical Semantics

回顾之前的章节用一串字母或者一个索引表示meanning of a word，如大写的CAT表示猫。

词元和词义:举例mouse这个词元，它有多个不同的含义，使解释变得困难。

同义词（Synonymy）: 举了一些同义词的例子，这里对同义词的定义挺有意思的: “两个词如果可以在任何句子中互换而不改变句子的真值条件，即句子为真的情况，那么这两个词就是同义词。”，但是在实践中，没有两个词的意义是绝对相同的， 同义词这个词被用来描述一种近似的或大致的同义关系。

词相似度（Word Similarity）: 虽然词语没有很多同义词，但大多数词语确实有很多相似词。猫不是狗的同义词，但猫和狗确实是相似词。

词相关性（Word Relatedness）: 词语之间存在关联但不一定相似的关系，在心理学中也称为词联想。比如咖啡和杯子。 根据是否属于同一个semantic field判断， 举了field of hospital， field of restaurants的例子。

含义（Connotation）: 我觉得这个和情感分析有关了， 举例积极的词（great， love） 和消极的词 （terrible， hate）。 然后指出Osgood这篇论文用Valence， arousal， dominance这三个指标去评价一个词， 这种革命性的观点认为词义可以被表示为空间中的一个点（例如，“心碎”的部分意义可以表示为点[2.5， 5.7， 3.6]），这是我们将要介绍的向量语义模型的首次表达。

5.2 Vector Semantics

提出了一个观点， 假如我们不知道Ongchoi的含义， 可以根据它的上下文去获取一些信息。

在这里不用在乎embedding是怎么做的， 只需要知道它可以实现从一个空间或结构到另一个空间或结构的映射， word2vec 算法的结果显示相似词汇在高维空间中彼此靠近

5.3 Simple count-based embeddings

从一个最简单的数学模型word-context matrix开始， 在该矩阵中，每一行代表词汇表中的一个词，每一列则表示词汇表中其他每个词在附近出现的频率。该矩阵的维度为|V|×|V|

对”附近”的定义是前后n=4个词， 实践中词汇表大小通常是10000到50000， 因为大部分值为0， 是稀疏矩阵表示， 可以高效存储。

5.4 Cosine for measuring similarity

为了衡量两个目标词v和w之间的相似性，我们需要一个度量标准， 最常见的相似性度量是向量之间夹角的余弦值。

从线性代数中的点积运算引导出cosine， 其实就是归一化的卷积， 然后也举了两个例子要怎么计算

$$\text{cosine}(\mathbf{v}, \mathbf{w}) = \frac{\mathbf{v} \cdot \mathbf{w}}{\lVert \mathbf{v} \rVert \lVert \mathbf{w} \rVert} = \frac{\sum_{i=1}^{N} v_i w_i}{\sqrt{\sum_{i=1}^{N} v_i^2}\sqrt{\sum_{i=1}^{N} w_i^2}}$$

5.5 Word2vec

回顾一下基于计数的嵌入， 每个word的维度是词汇表长度， 现在引入embeddings， 与我们迄今为止看到的向量不同，embeddings是短的，维度d范围从50到1000，直觉告诉我们密集向量都比稀疏向量表现得更好， 较小的参数空间可能有助于泛化并避免过拟合

介绍了一种常见的常见的方式SGNS， 属于静态嵌入， 有时候就把这种算法称作word2vec。 与其统计每个词w在比如说杏子（apricot）附近出现的频率，不如在一个二元预测任务上训练一个分类器：“词w是否可能出现在杏子附近？”我们实际上并不关心这个预测任务；相反，我们会将学习到的分类器权重作为词嵌入。

5.5.1 The classifier

我们这样定义概率， P(+|w, c)为上下文词（context word）c是目标词w的真实上下文词的概率（文中取上下文窗口为2）。 现在我们的问题是怎么计算这个概率， Skip-gram 模型的直觉是: 一个词的上下文词在语义空间中应该与它的嵌入向量相似。 也就是说， 如果两个词的嵌入向量相似， 那么它们很可能在上下文中一起出现。 很容易想到用点积去衡量两个word的相似度 $Similarity(w, c) \approx \mathbf{c} \cdot \mathbf{w}$， 值域是0到1， 接着用sigmoid函数缩放到0到1的概率， 推导出的公式为:

$$P(+|w, c) = \sigma(\mathbf{c} \cdot \mathbf{w}) = \frac{1}{1 + \exp(-\mathbf{c} \cdot \mathbf{w})}$$

还可以拓展到多个上下文词

$$P(+|w, c_{1:L}) = \prod_{i=1}^{L} \sigma(\mathbf{c}_i \cdot \mathbf{w})$$

取对数后

$$\log P(+|w, c_{1:L}) = \sum_{i=1}^{L} \log \sigma(\mathbf{c}_i \cdot \mathbf{w})$$

5.5.2 Learning skip-gram embeddings

Skip-gram 嵌入的学习算法以一个文本语料库和一个指定的词汇表大小N 为输入。

它首先为词汇表中每个词随机分配一个嵌入向量，然后通过迭代更新，使得每个目标词w 的嵌入更接近出现在它附近的词的嵌入，同时远离那些不在其附近出现的词的嵌入。

从一个大型语料库中， 对于目标词w， 相邻的上下文词 $c_+$， (w, c*+)称为一个真样本， 同理(w, $c*-$)称为一个负样本， 有几个参数控制训练数据， k=负样本数/正样本数， 控制正负样本比例，

α控制不同词被采样的概率， 为了理解这个概念， 要从负样本的制作说起， 正样本好说， w周围的 $c_+$就那么几个， 但是 $c_-$却有很多， 选择哪个 $c_-$需要抉择， 当α为1时按照词频采样， 根据每个词出现的频率计算一个被抽到的概率， 但是这样稀有词很难被抽到， 因此引入α， α越小， 每个词被抽取的概率越平均。

定义损失函数

$$L = -\log P(+|w, c_{pos}) - \sum_{i=1}^{k} \log P(-|w, c_{neg_i})$$

这里的P(-|w,c)前面没有提， P(-|w,c)+P(+|w,c)=1

然后优化这个损失函数L用的SGD， 学习率控制w，c更新速率， 推导有点复杂， 贴一个结果吧。

5.5.3 Other kinds of static embeddings

介绍fasttext方法， 优化了对未见词， 罕见词的处理; 介绍GloVe方法， 基于词-词共现矩阵中的概率比值。

5.6 Visualizing Embeddings

介绍了几种可视化方法， 1） 算余弦， 列出与w最相似的词。 2） 使用聚类算法来展示嵌入空间中哪些词与其他词相似的层次表示。 3） 将一个词的100个维度投影到2个维度（t-SNE）

5.7 Semantic properties of embeddings

Different types of similarity or association。 当向量从短上下文窗口计算时，目标词w最相似的词往往是具有相同词性的语义相似词。当向量从长上下文窗口计算时，与目标词w余弦相似度最高的词往往是主题相关的但并不相似的词。

Analogy/Relational Similarity。 举了一个平行四边形的例子， apple:tree::grape:?， 就是下面这个图， 根据嵌入矩阵， grape:vine， 最后指出这种方法过于简单， 无法模拟人类形成此类类比的认知过程。

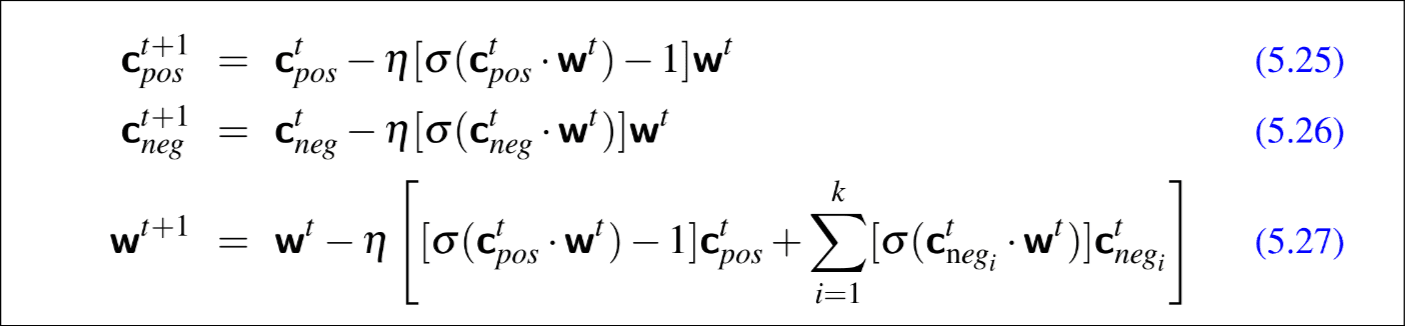
嵌入也可以成为研究意义随时间变化的有用工具

5.8 Bias and Embeddings

举了一些例子， “king”-“man”+“woman”=“queen”， “doctor”-“father”+“mother”=“nurse”， 也举了一些偏见的例子， 像‘computer programmer’ - ‘man’ + ‘woman’ = ‘homemaker’， 说明嵌入放大了偏见。

嵌入也编码了人类推理中隐含关联的属性。举例，像“Leroy”和“Shaniqua”这样的非裔美国人名字与不愉快的词语有更高的GloVe余弦值，而欧裔美国人名字（如“Brad”，“Greg”，“Courtney”）则与愉快的词语有更高的余弦值。

一些研究尝试消除这些偏见， 历史嵌入也被用来衡量过去的偏见。

5.9 Evaluating Vector Models

内在评估: 1）计算算法的词相似性得分与人类给出的词相似性评分之间的相关性; 2）语义文本相似性任务; 3）类比任务